News
- 2025年10月24日 解説記事
- ノーコード機械学習・AIアプリeasy-MIを使ってみる!
マテコン(Material Consultant)が提供している,プログラミングなしで機械学習・AIが実行可能な完全無料アプリeasy-MIを使ってみましょう!
この記事では,簡単な使い方を解説します。まずは,easy-MI(https://www.easy-mi.jp)にアクセスして,以下のGIF動画をご覧ください。

操作は簡単。
❶ 練習用データセットをダウンロード
❷ データセットをアップロード
❸ 目的変数(機械学習で予測するターゲット)を選択
❹ 説明変数(予測に使用する変数)を選択
❺ 処理の選択→「前処理」,前処理方法→「標準化」をそれぞれ選択
❻ 処理の選択→「回帰」,回帰モデルの選択→「最小二乗法(OLS)」を選択
❼ 実行ボタン(Runボタン)をクリック
今回は上記の操作のみです。それでは順を追って説明していきます。
❶ 練習用データセットをダウンロード
easy-MIにアクセスして,「インク組成のデータセット (練習用)」をダウンロードボタンからダウンロードしましょう。
データセット(ink.csv)には,インク組成に対する物性値が100 サンプル分,記載されています。
物性値:
- Viscosity(粘度): インク/塗料の粘度(単位: cP)
- Adhesion(密着性): 塗膜の密着性評価(0~25,数値が高いほど良い)
- Pot Life(ポットライフ): インク/塗料の調液から2年後の粘度変化率(単位: %)
- pH: インク/塗料のpH
インク組成:
- Pigment(顔料): インク/塗料内の質量%(単位: wt%)
- Dispersant(分散剤): 顔料の分散剤,インク/塗料内の質量%(単位: wt%)
- Binder 1(バインダー1): 塗膜化するための樹脂1,インク/塗料内の質量%(単位: wt%)
- Binder 1 Contents(バインダー1含有物): バインダー1を合成するために特別に使用されたもの(単位: 使用された場合1,使用されていない場合0)
- Binder 2(バインダー2): 塗膜化するための樹脂2,インク/塗料内の質量%(単位: wt%)
- Binder 2 Contents(バインダー2含有物): バインダー2を合成するために特別に使用されたもの(単位: 使用された場合1,使用されていない場合0)
- Crosslinker(架橋剤): バインダーを架橋するためのもの,インク/塗料内の質量%(単位: wt%)
- Solvent A(溶剤A): インク/塗料にするための水溶性溶剤,インク/塗料内の質量%(単位: wt%)
- Solvent B(溶剤B): インク/塗料にするための水溶性溶剤,インク/塗料内の質量%(単位: wt%)
- Water(脱イオン水): インク/塗料を調液に使用する脱イオン水,インク/塗料内の質量%(単位: wt%)
❷ データセットをアップロード
easy-MIにダウンロードしたファイル(ink.csv)をアップロードしてください。アップロード方法がわからない方は,このページの初めにある動画(GIF)を見てください。たぶんできます。。。
データをアップロードすると,データセットタブにデータセットのプレビューが表示されます。
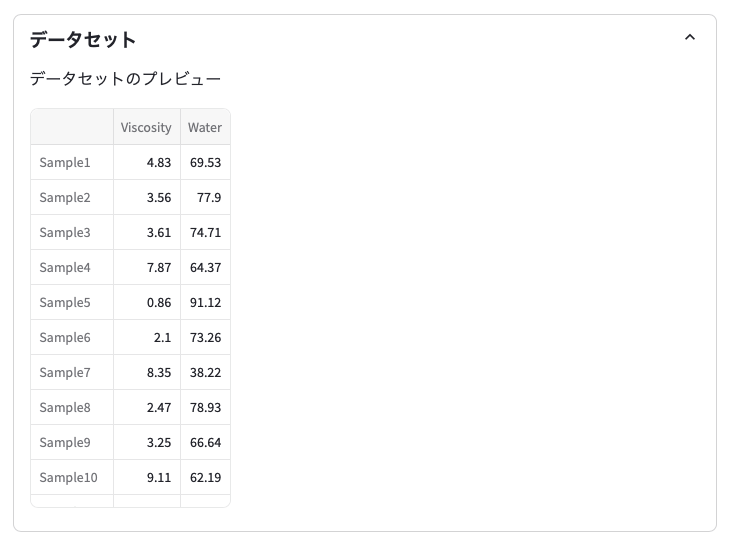
❸ 目的変数(機械学習で予測するターゲット)を選択
目的変数を選択してください。目的変数とは,予測対象となる変数のことです。
つまり,y = axの’y’です。
今回は,目的変数yに「Viscosity」を選択してください。

インクの粘度(Viscosity)をインク組成から予測していく機械学習モデルを構築していきます。
❹ 説明変数(予測に使用する変数)を選択
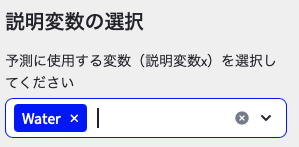
説明変数を選択してください。説明変数は予測するために使用する変数であり,y=axの’x’にあたります。まずは,説明変数に「Water」を選択してください。
❸目的変数を選択の時点で,説明変数が自動で選択されていると思いますが,「Water」以外はすべて削除してください(下の図のような状態にしてください)。
すると,easy-MI画面内のデータセットには,「Viscosity」「Water」の順に表示されているはずです。
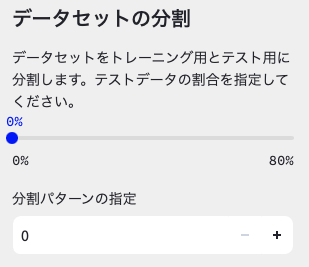
次に,データセットの分割は0%にしましょう。←ここは後で説明します。
初期は30%になっています。分割パターンはそのまま「0」で問題ありません。
❺ 処理の選択→「前処理」,前処理方法→「標準化」をそれぞれ選択
ここでは,データの「標準化」を行います。
標準化(Standardization)とは,データのスケール(値の大きさの単位)をそろえる処理のことです。
今回の場合には
- 「Water」の単位は%で,数値が 0〜100 の範囲
- 「Viscosity」の単位はcPで,2~15の範囲
というように,変数ごとにスケールが大きく異なる場合があります。
このままだと,数値の大きい変数が機械学習モデルに強く影響してしまうことがあります。
そのため,標準化によって各変数を「平均0」「標準偏差1」に変換し,すべての変数が同じ基準で扱われるようにします。
easy-MI上では,解析アルゴリズムの選択タブにて,「処理の選択」→「前処理」を選択した後に,「前処理方法」→「標準化」を選択してください。通常の場合であれば,説明変数(x),目的変数(y)どちらも標準化しておいて問題ありません。ですので,「説明変数に標準化を実行する」「目的変数に標準化を実行する」ともにチェックしたままにしましょう。
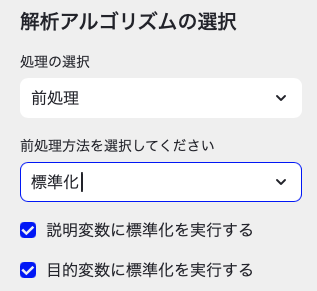
easy-MIのメイン画面には,標準化というタブが表示されているはずです。タブをクリックすると,標準化の計算結果が表示されるので確認してみてください。
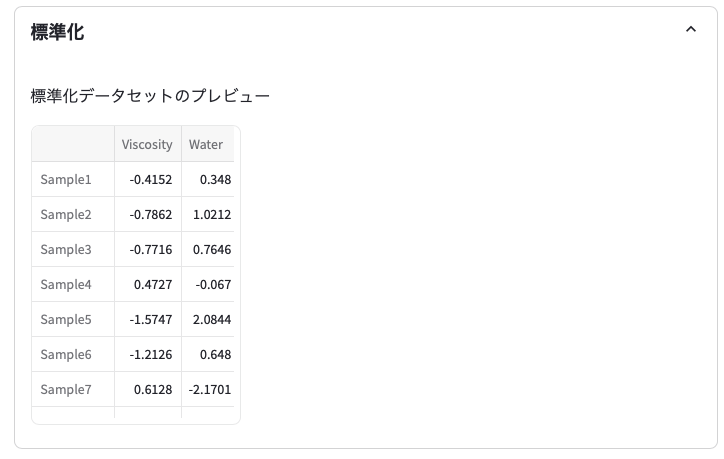
❻ 処理の選択→「回帰」,回帰モデルの選択→「最小二乗法(OLS)」を選択
次に,実際に予測モデルを作成してみましょう。
この記事では,予測モデルとして最小二乗法(OLS)を使用します。
■ OLSとは?
最小二乗法(OLS: Ordinary Least Squares)は,最も基本的な回帰分析の方法で,データの関係「直線(一次式)」で表すモデルです。数式で書くと次のようになります。
y = a0 + a1x1 + a2x2 + ⋯ + anxn + b
説明不要かもしれませんが,y,x,aは以下です。
- y : 目的変数(今回ならViscosity)
- x1, x2, … : 説明変数(今回ならWater)
- a1, a2 … : 学習によって求められる係数
- b: 切片
今回は「Water」1つだけを説明変数とした単回帰ですので,式はシンプルになります。
yViscosity = aWater・xWater + b
OLSでは、予測値と実測値の差(誤差)をできるだけ小さくするように,a(傾き)とb(切片)を求めます。
この「誤差の二乗和(Σ(予測値 − 実測値)2)」を最小にすることから,「最小二乗法(Ordinary Least Squares)」と呼ばれています。
ちなみに,この式にある切片bは,標準化を行っている場合ほとんど意味を持ちません。
今回のように,説明変数,目的変数の標準化によって,すべての変数の平均が0にそろえられるため,モデルは「原点を通る直線」に近い形になります。
その結果,切片はほぼ0になります。
要するに,標準化をしていれば,bはゼロだと思ってOKです。
もちろんデータの丸め誤差などでわずかにずれることはありますが,モデルの意味合いとしてはほとんど影響ありません。
それでは,easy-MI上の画面でOLSモデルを選択しましょう。
先ほど選択した「標準化」の下に,処理の選択を「回帰」に,「回帰モデルの選択」は「最小二乗法(OLS)」を選択しましょう。回帰モデルを選択すると,「モデルの評価基準の選択してください」という新しいプルダウンメニューが表示され,デフォルトでは「決定係数(R2)」となっています。いくつか評価基準を用意していますが,決定係数(R2)のままで問題ありません。
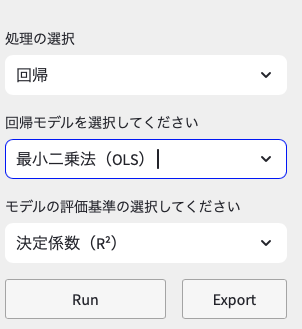
❼ 実行ボタン(Runボタン)をクリック
最後に,実行ボタンをクリックしてください。OLSは計算スピードが速いのですぐに結果が表示されるはずです。
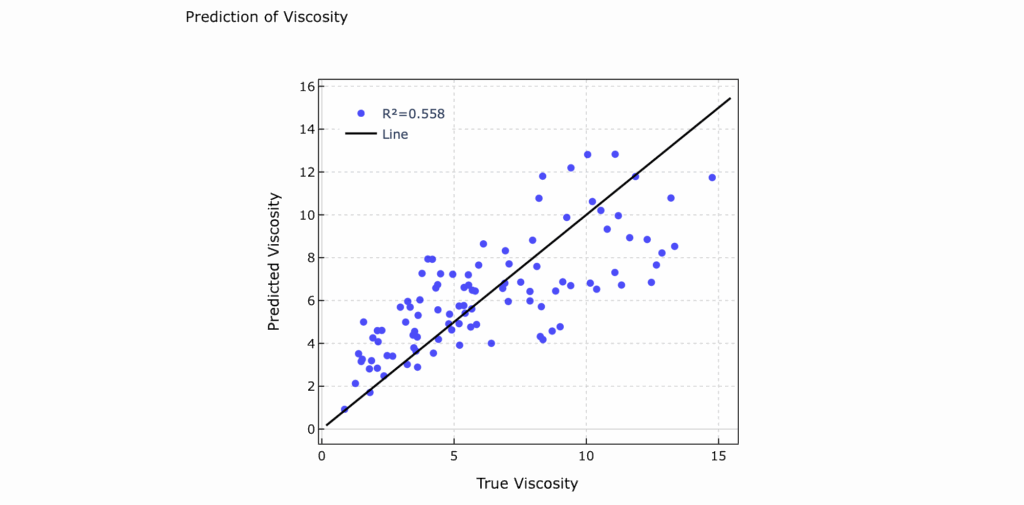
easy-MIのメイン画面には,「最小二乗法(OLS)のプレビュー」「最小二乗法(OLS)の回帰係数」「最小二乗法(OLS)の予測精度」の3つのグラフが表示されています。
「最小二乗法(OLS)のプレビュー」では,横軸が「True Viscosity」,縦軸「Predicted Viscosity」となっており,横軸に実験値(測定値),縦軸にはOLSモデルによって予測された値が示されています。黒の斜線(Line)は,傾き1の基準線でして,このLineにプロットが近ければ近いほど,予測精度は高い=決定係数(R2)値が1に近い,ということになります。今回の予測では,決定係数(R2)が0.558で予測されています。
「最小二乗法(OLS)の回帰係数」では,Waterの棒グラフが-0.75を示しています(棒グラフにマウスを合わせてみてください)。
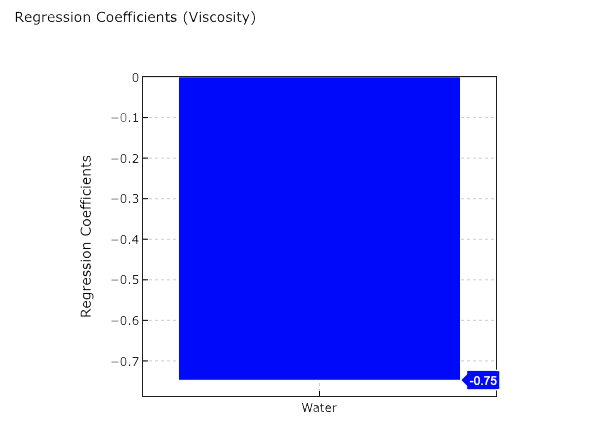
これは,xWaterの係数aが-0.75ということであり,つまり今回のOLSモデルは以下になります。
yViscosity = -0.75xWater
標準化しているので,bはほぼゼロと考えてよいでしょう。
「最小二乗法(OLS)の予測精度」では,画面を横にスルロールすると,決定係数(R2)だけでなく,二乗平均平方根誤差(RMSE)や平均絶対値誤差(MAE)が表示されているので確認してみてください。それぞれの評価基準について興味のある方は調べてみると良いでしょう。
■ 説明変数を増やしてみる(重回帰)
ここまでの例では,Water(脱イオン水)のみを説明変数に使用して,Viscosity(粘度)を予測する単回帰モデルを作成しました。しかし,実際のインク組成には,Pigment(顔料)やBinder(バインダー)など,粘度に影響しそうな要素がたくさんあります。これらを説明変数に加えることで,より精度の高い予測モデル(重回帰モデル)を構築できます。
操作手順は先ほどと同様ですが,目的変数は「Viscosity(粘度)」をそのままにして,説明変数にインク組成を加えてください。
❹ 説明変数を再選択 → 「Pigment(顔料)」「Dispersant(分散剤)」「Binder 1(バインダー1)」「Binder 1 Contents(バインダー1含有物)」「Binder 2(バインダー2)」「Binder 2 Contents(バインダー2含有物)」「Crosslinker(架橋剤)」「Solvent A(溶剤A)」「Solvent B(溶剤B)」「Water(脱イオン水)」を選択しましょう。
❺ 処理の選択→「前処理」,前処理方法→「標準化」をそれぞれ選択
❻ 処理の選択→「回帰」,回帰モデルの選択→「最小二乗法(OLS)」を選択
❼ 実行ボタン(Runボタン)をクリック
実行ボタンを押すと,以下の回帰式が得られます。
yViscosity = aPigment・xPigment + aDispersant・xDispersant + ・・・+ aWater・xWater
標準化しているので,各変数の単位が揃っており,係数の絶対値が大きい変数ほど影響度が強いと解釈できます。
「最小二乗法(OLS)のプレビュー」を確認すると,決定係数(R²)は 0.840。
先ほどの「Water(脱イオン水)」のみを説明変数とした場合に比べ,予測精度が大幅に向上していることがわかります。
これは,粘度(Viscosity)に影響を与える複数のインク組成成分を説明変数として追加したことで,精度の高いモデルが構築されたためです。

それでは,どのインク組成が粘度の予測に強く寄与しているのかを見てみましょう(回帰係数を確認しましょう)。
最小二乗法(OLS)の回帰係数のグラフを確認すると,各変数の棒グラフが表示されています。
標準化を行っているため,係数の絶対値が大きいほど,その変数が粘度(Viscosity)に強い影響を与えていると解釈できます。
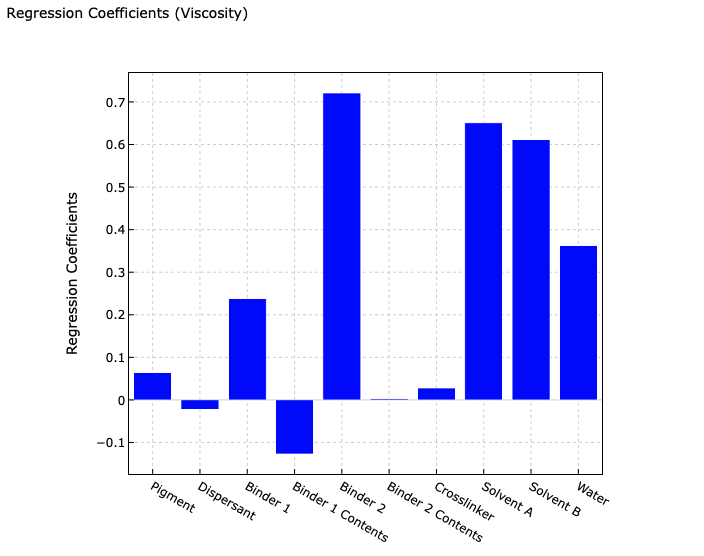
したがって,「Binder 2(バインダー2)」「Solvent A(溶剤A)」「Solvent B(溶剤B)」「Water(脱イオン水)」が粘度(Viscosity)に値を寄与していることが読み取れます。このモデルの決定係数は0.8を超えて十分に高いので,信頼できるモデルと考えられますし,バインダーや溶剤がインクの粘度に効くのは原理原則的にも妥当でしょう。
■ データの分割
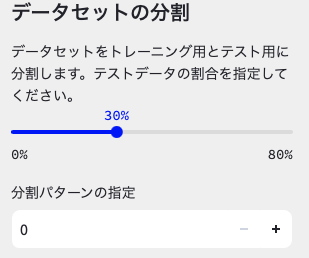
最後にデータセットをトレーニングデータとテストデータに分割してみましょう。
手順は,データセットの分割箇所を「30%」にするのみです。分割パターンは0のままで大丈夫です。
説明変数は「Pigment(顔料)」「Dispersant(分散剤)」「Binder 1(バインダー1)」「Binder 1 Contents(バインダー1含有物)」「Binder 2(バインダー2)」「Binder 2 Contents(バインダー2含有物)」「Crosslinker(架橋剤)」「Solvent A(溶剤A)」「Solvent B(溶剤B)」「Water(脱イオン水)」のままです。
データセットの分割に成功すると,データの分割タブが表示されます。データの分割タブは普段は閉じているので,クリックするとタブが開き,トレーニングデータとテストデータが表示されます。
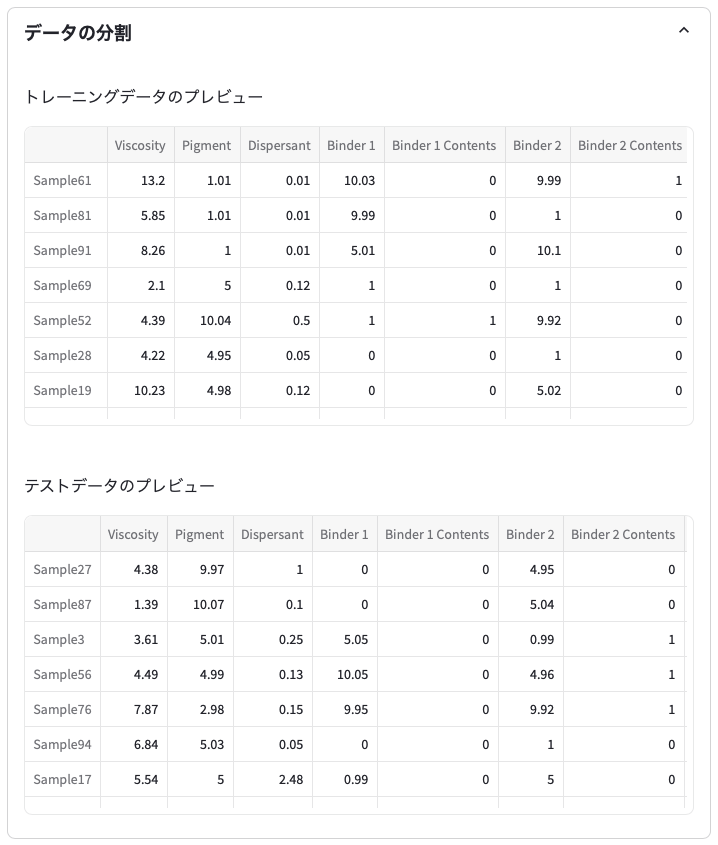
分割パターンの数値を変更すると,データセットの分割パターンが変化します。トレーニングデータにあるサンプル組み合わせと,テストデータにあるサンプルの組み合わせが変わります。
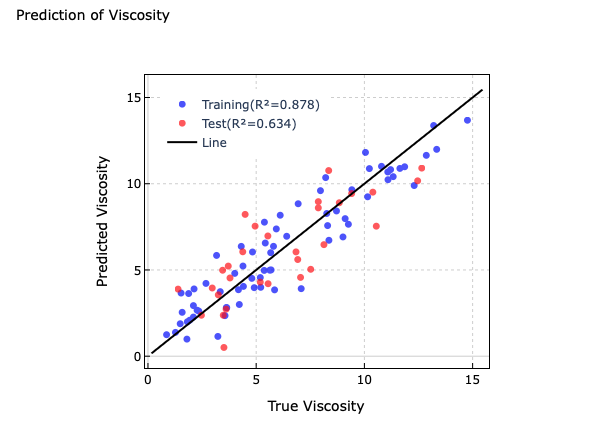
それでは,分割パターンを「0」にして実行ボタン(Runボタン)を押してみてください。最小二乗法(OLS)のプレビューを確認すると,トレーニングデータが決定係数(R2)= 0.878,テストデータが決定係数(R2)= 0.634となっていることがわかると思います。
なぜデータセットを分割するのか?
データを分割する理由は,モデルが新しいデータ(未知データ)においても,しっかり予測できるか確かめるためです。すべてのデータを使って学習してしまうと,データの”丸暗記”になってしまい,未知のデータではうまく予測できなくなることがあります。これを過学習と呼びます。
そこで,今回はデータセットを
- トレーニングデータ(約70%):モデルを学習する用
- テストデータ(約30%):モデルの実力を試す用
に分けて評価しました。分割はトレーニングデータ: テストデータ = 7:3が通常で,データセット数が少なければ,8:2や9:1を試してみるのが良いでしょう。
今回のように,トレーニングデータで R²=0.878、テストデータで R²=0.634 くらいの差であれば,過学習は起きておらず,モデルはまずまず良い汎化性能(=新しいデータにも対応できる力)を持っているといえます。
easy-MIでは「分割パターン」の数値を変えることで,データの組み合わせを変えることができます。どのパターンでも結果が大きく変わらなければ,モデルは安定していると判断できます。
分割パターンを変更しても,テストデータの精度がおよそ0.6ぐらいになるはずです。つまり,このモデルの精度はR2=0.6程度であると言えるでしょう。
easy-MIでは,最小二乗法(OLS)以外にも,様々な機械学習モデルを提供しいますので,気軽に使用してみてください。
